목차
Tree ?
Tree의 종류
- Binary Tree
- Binary Search Tree
- Complete Binary Tree
- Full Binary Tree
- Perfect Binary Tree
Binary Tree 3가지 순회방법
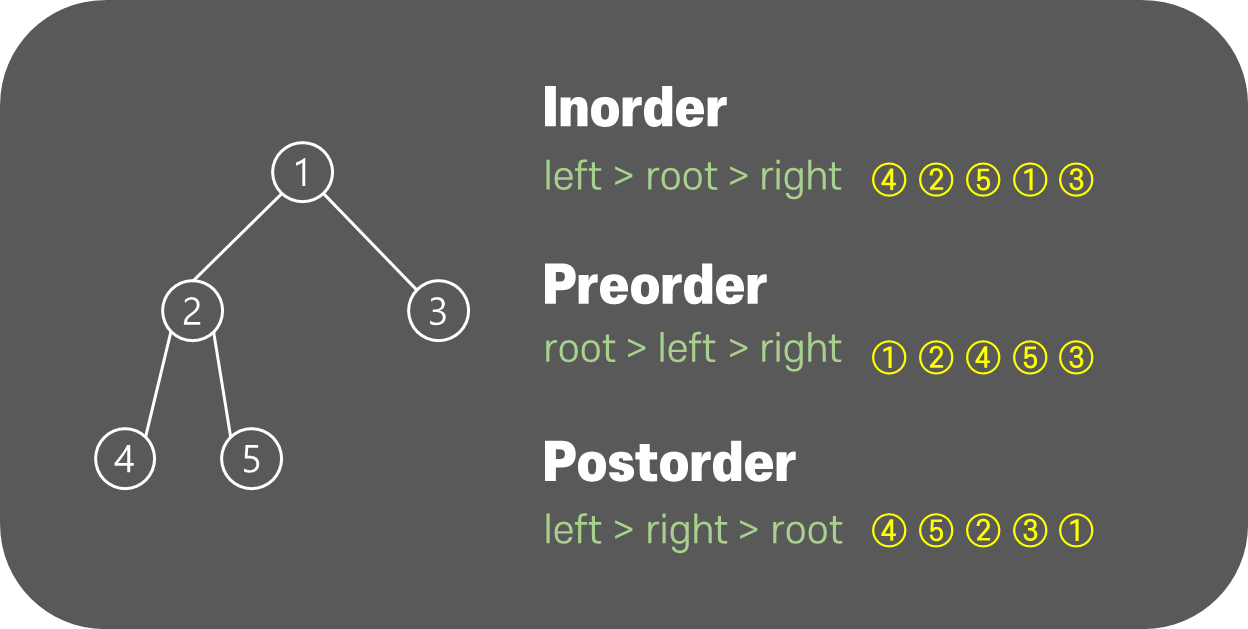
- Inorder (Left, Root, Right)
- Preorder (Root, Left, Right)
- Postorder (Left, Right, Root)
Tree ?
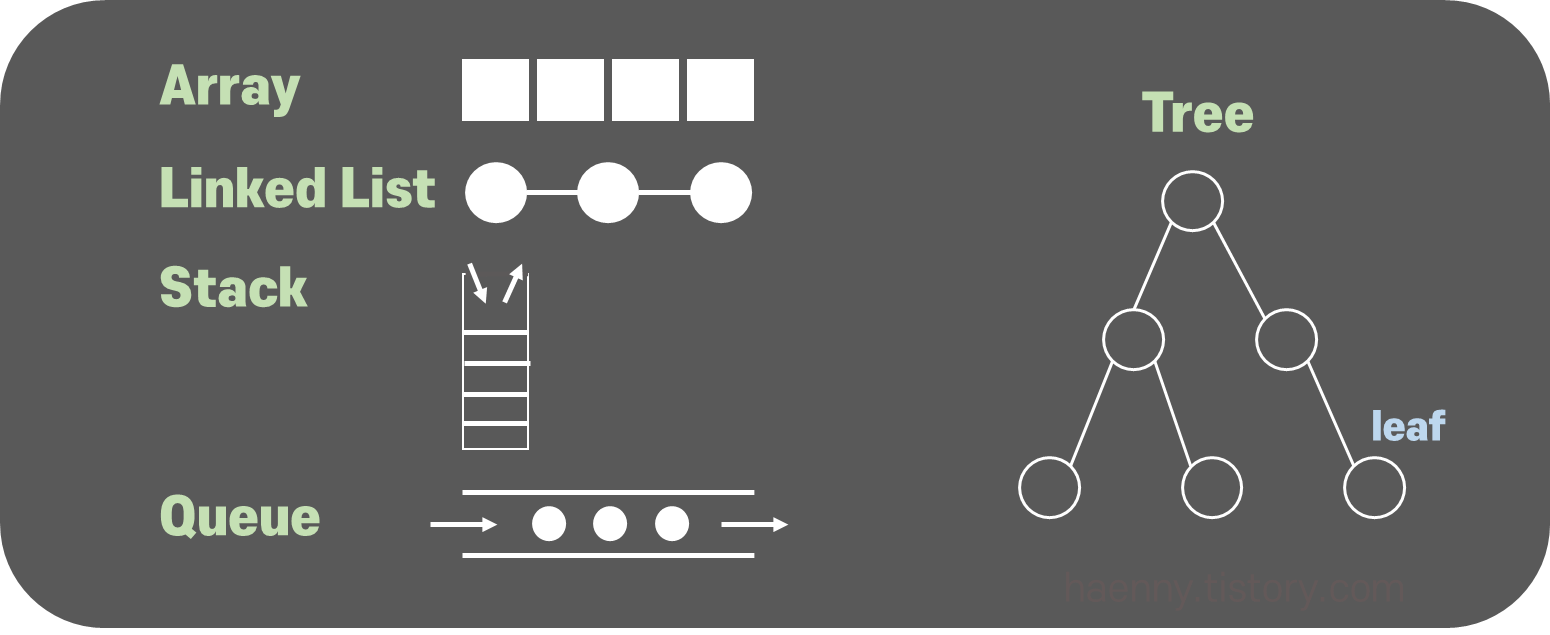
그 동안 많이 접해왔던 Array, LinkedList, Stack, Queue 와 같이 라인처럼 생긴 일직선 데이터들이 있다면,
트리(Tree)는 부모 자식 관계를 가지는 구조이며, 계층과 그룹이 있다.
각 노드(Node)는 하나 이상의 자식을 갖고 있다.
트리(Tree) 노드(Node) 중에는 부모를 아는 경우가 있고, 자식만 아는 경우가 있고, 어떤 특정한 순서에 의해 관리되는 경우도 있다.
트리(Tree)의 맨 끝에 더 이상의 자식이 없는 마지막 노드를 Leaf (잎사귀)라고 부른다.
Tree의 종류
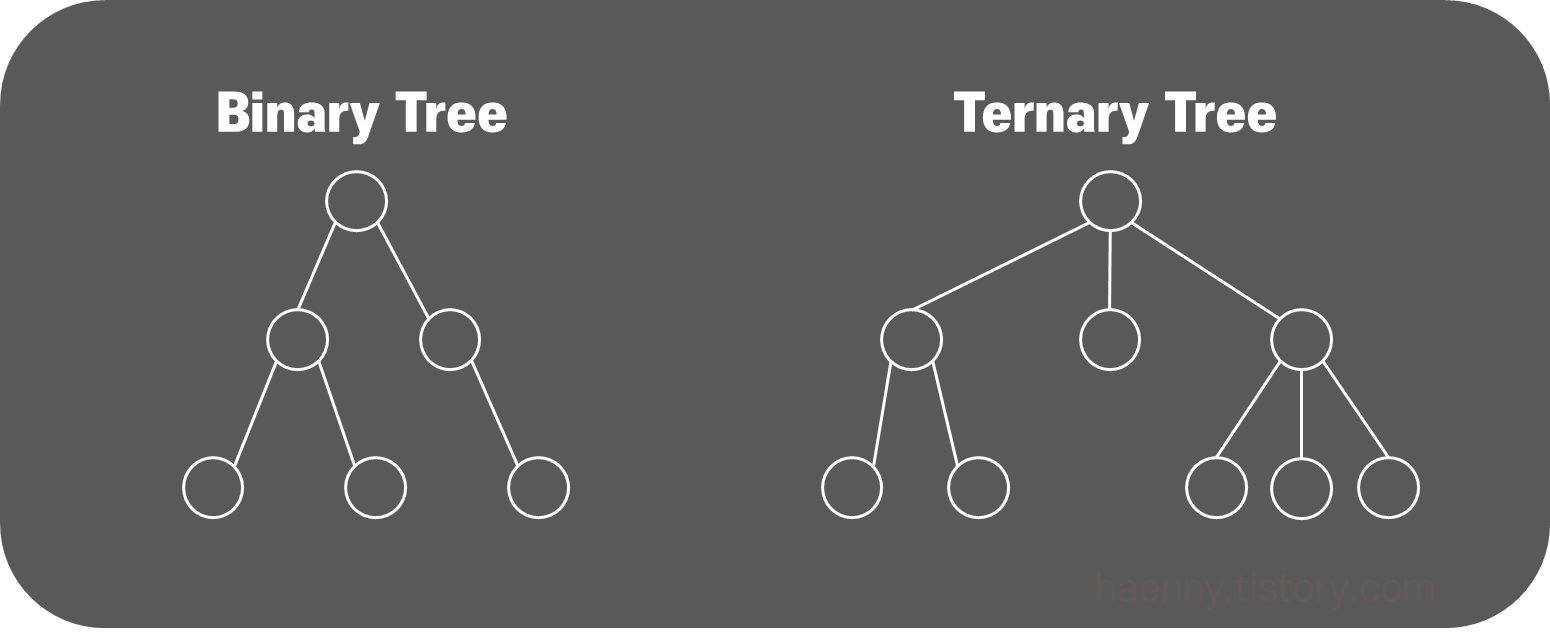
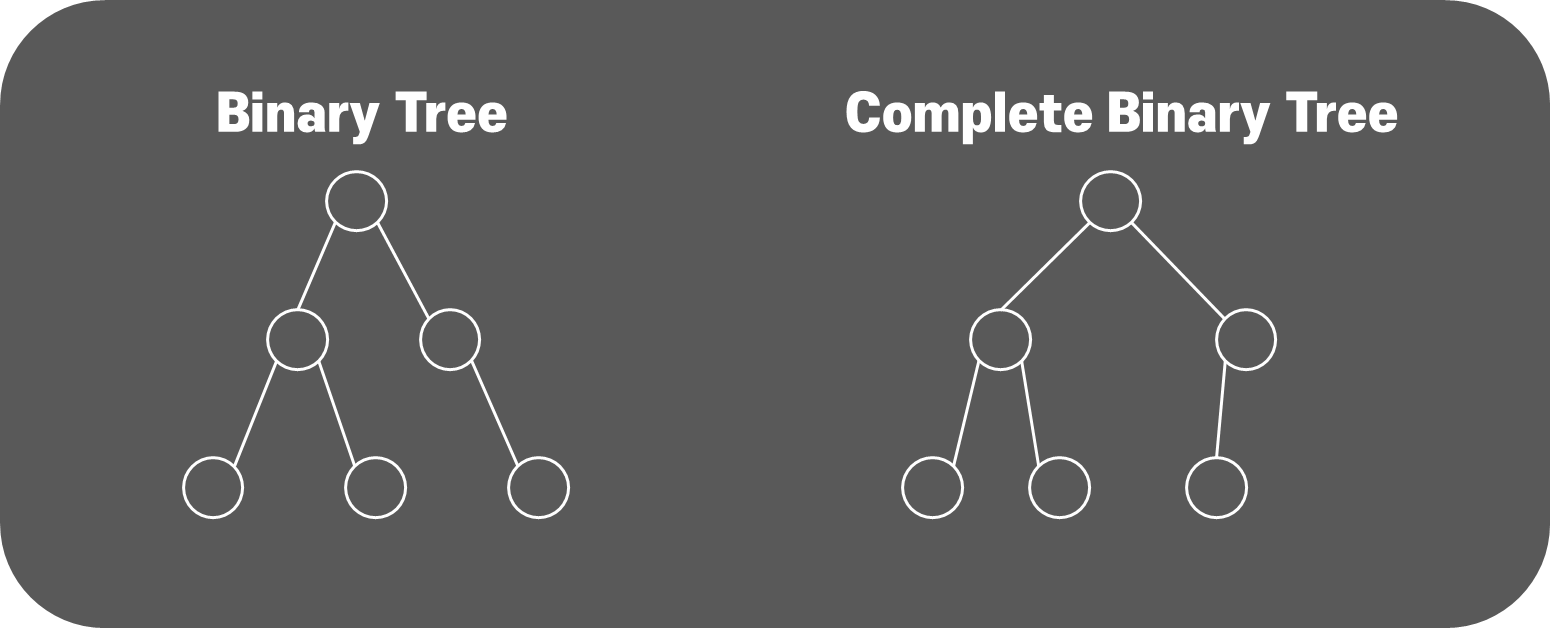
Binary Tree (이진 트리)
자식노드가 최대 2개까지만 붙는 트리로, 알고리즘에서 가장 관심을 갖고 공부하는 트리이다.
마찬가지로 자식노드가 최대 3개까지 붙는 트리는 Ternary Tree라고 한다.
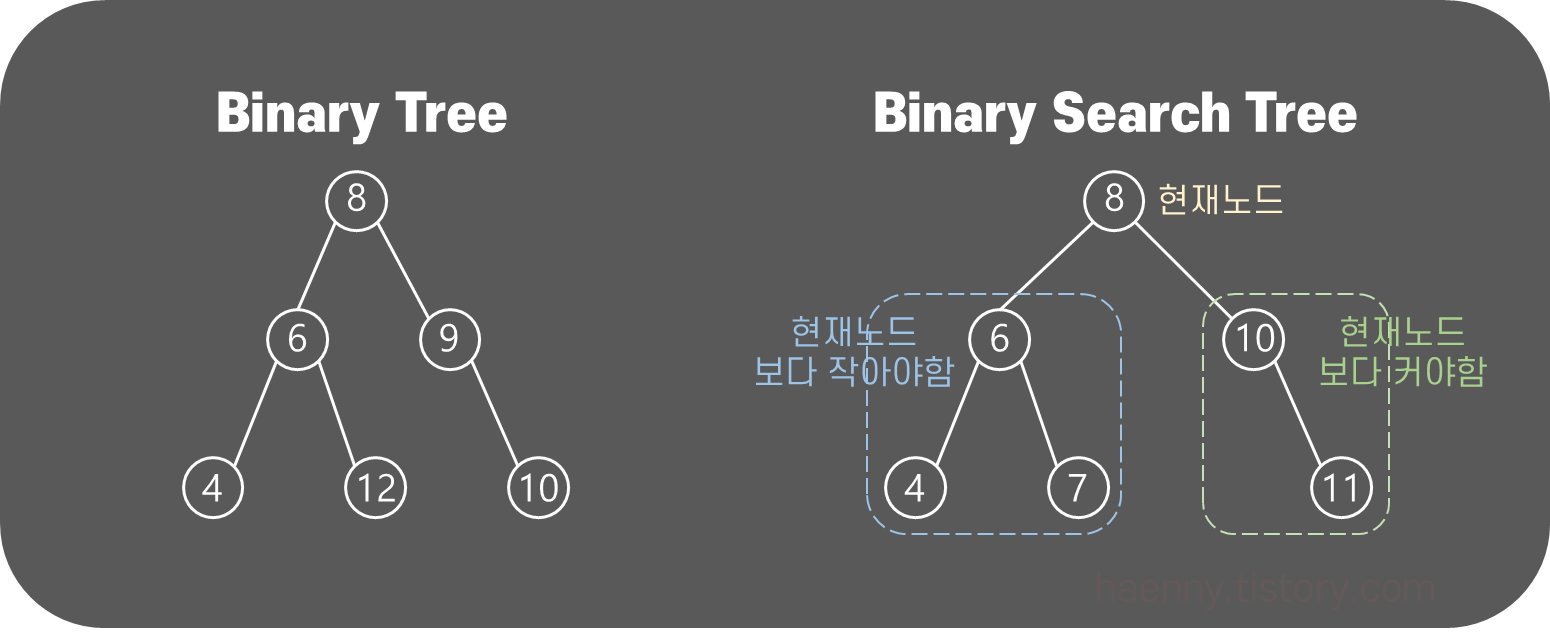
Binary Search Tree (이진 검색 트리)
binary tree (이진 트리)의 데이터가 왼쪽 노드와 그 이하 자식노드는 현재 노드보다 작아야하고, 오른쪽 노드와 그 이하 자식노드는 현재 노드보다 커야한다.
현재 노드보다 큰 값을 찾고 싶으면 오른쪽, 작은 값을 찾고 싶으면 왼쪽 노드를 가야하는 것!
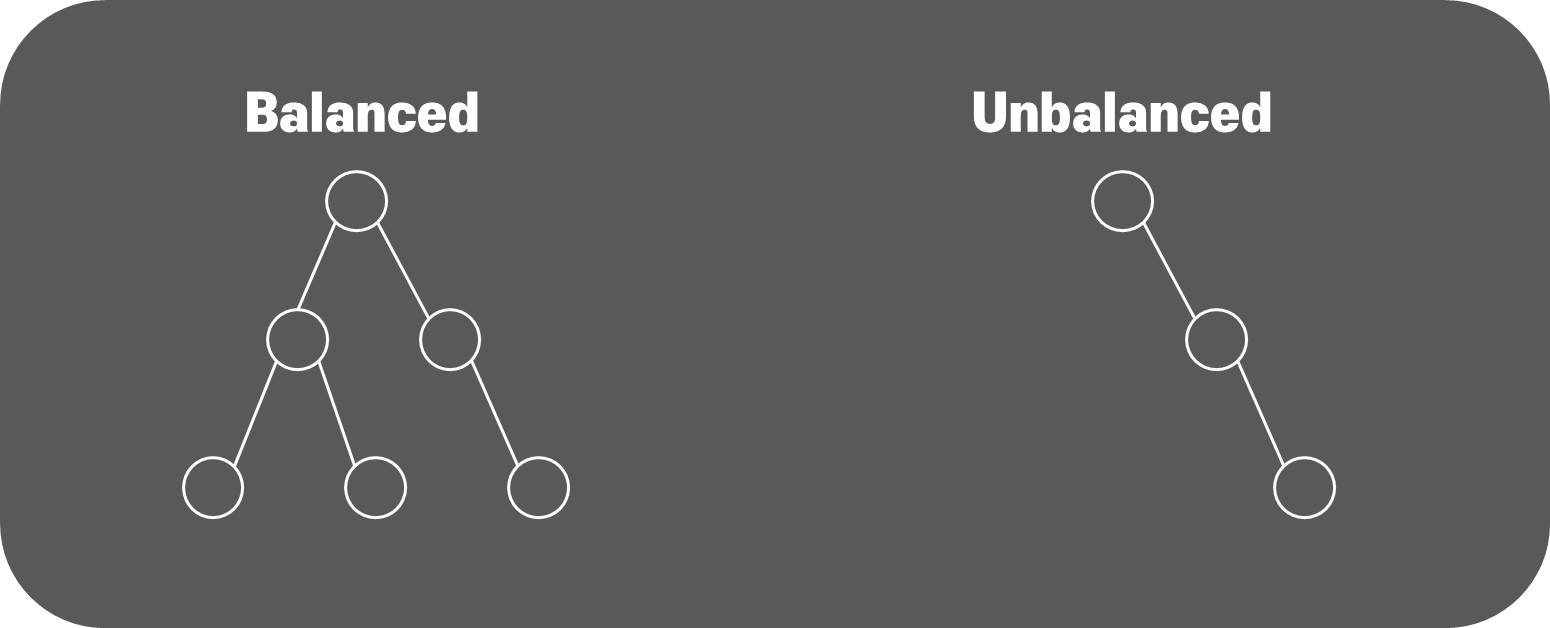
Balance
트리(Tree)에서 발란스가 맞다 안맞다는 노드의 갯수가 맞다 안맞다가 아닌 노드가 치우치지 않는 정도로 생각하면 된다.
balance가 맞는 대표적인 트리
- Red-black Tree
- AVL Tree
Complete Binary Tree (완전 이진 트리)
모든 서브트리의 레벨이 같고, 모든 노드들이 레벨별로 왼쪽부터 채워져있는 경우
Full binary Tree
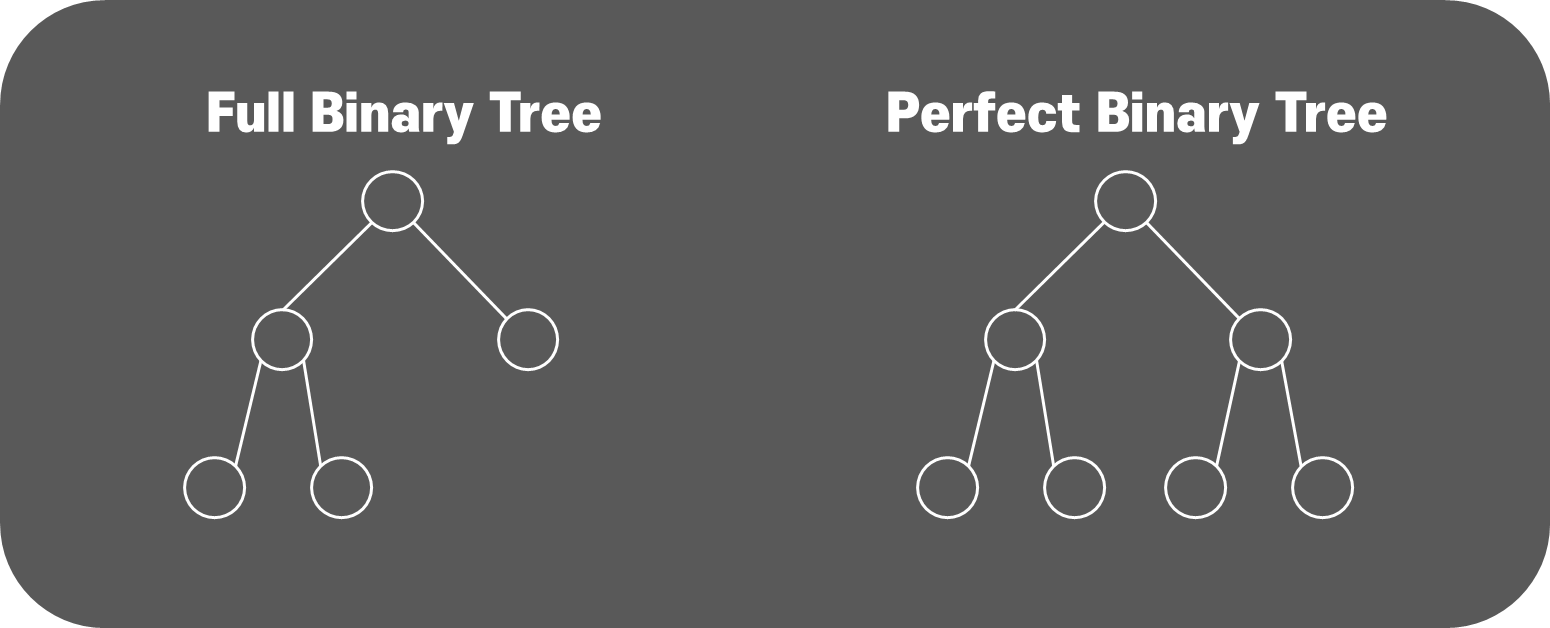
자식 노드를 한 개도 안 갖고 있거나, 자식이 있는 경우는 두 개의 자식을 갖는 경우
Perfect binary Tree
양쪽으로 빈 공간 없이 모든 노드가 두개의 자식을 갖고, 레벨도 정확하게 떨어지는 트리.
완벽한 파라미드 구조를 형성하고 있음
레벨이 n인 경우, 노드의 개수는 2ⁿ-1 개이다
Binary Tree 3가지 순회방법
class Node { // binary tree node
int data;
Node left; // left child node
Node right; // right child node
}
class Tree {
// root node 와 get, set
public Node root;
public void setRoot(Node node) {
this.root = node;
}
public Node getRoot() {
return root;
}
// node 생성 (left child node, data, right child node)
public Node makeNode(Node left, int data, Node right) {
Node node = new Node();
node.data = data;
node.left = left;
node.right = right;
return node;
}
// inorder
public void inorder(Node node) {
// node가 null이 아닐 때까지 재귀호출 반복
if(node != null) {
// left node 재귀호출을 다 돌고난 후 > 자기 자신 출력 > right node 재귀호출
inorder(node.left);
System.out.println(node.data);
inorder(node.right);
}
}
public void preorder(Node node) {
// node가 null이 아닐 때까지 재귀호출 반복
if(node != null) {
// 자기 자신 출력 > left node 재귀호출을 다 돌고난 후 > right node 재귀호출
System.out.println(node.data);
preorder(node.left);
preorder(node.right);
}
}
public void postorder(Node node) {
// node가 null이 아닐 때까지 재귀호출 반복
if(node != null) {
// left node 재귀호출을 다 돌고난 후 > right node 재귀호출 > 자기 자신 출력
postorder(node.left);
postorder(node.right);
System.out.println(node.data);
}
}
}
public class Main {
public static void main (String[] args) {
Tree t = new Tree();
Node n4 = t.makeNode(null, 4, null);
Node n5 = t.makeNode(null, 5, null);
Node n2 = t.makeNode(n4, 2, n5);
Node n3 = t.makeNode(null, 3, null);
Node n1 = t.makeNode(n2, 1, n3);
t.setRoot(n1);
t.inorder(t.getRoot()); // 4 2 5 1 3
t.preorder(t.getRoot()); // 1 2 4 5 3
t.postorder(t.getRoot()); // 4 5 2 3 1
}
}'Algorithm > Tree & Graph' 카테고리의 다른 글
| [알고리즘] 세그먼트 트리(Segment Tree) 알고리즘 동작 원리 및 구현하기 (0) | 2022.10.26 |
|---|---|
| [알고리즘] 다익스트라 알고리즘 (Dijkstra Algorithm) 동작 원리 및 구현하기 (1) | 2022.07.07 |
| [자료구조] Binary Heaps (Min-Heap and Max-Heap) 간단하게 알아보기 (0) | 2022.06.05 |
| [자료구조] 그래프(Graph)의 개념 및 탐색 간단하게 알아보기 (1) | 2022.05.23 |


댓글