Heap ?
힙(Heap)은 이진 힙(Binary Heap)이라고도 하며, 최대 값이나 최소 값을 빠르게 구하기 위해 구현된 완전이진트리(Complete Binary Tree)를 기본으로 한 자료구조
힙(Heap)의 속성
- 완전 이진트리 (Complete Binary Tree)
- 부모 노드와 자식노드의 값 사이에 대소관계 성립 (형제노드사에의 대소관계는 정해지지 않음)
힙(Heap)의 종류
- 최소힙 (Min Heap) : 부모 노드가 자식 노드보다 항상 작은 값을 가지고 있고, 가장 작은 값이 루트(root)인 트리구조
- 최대힙 (Max Heap) : 부모 노드가 자식 노드보다 항상 큰 값을 가지고 있고, 가장 큰 값이 루트(root)인 트리구조
최소 힙의 노드 삽입하기
1. 완전이진트리에 맨 끝 노드에 노드를 추가한다. (완전이진트리를 잃지 않도록 마지막 노드 왼쪽부터 추가한다)
2. 노드를 추가한 뒤 정렬을 맞추기 위해 자신의 부모노드와 비교한다.
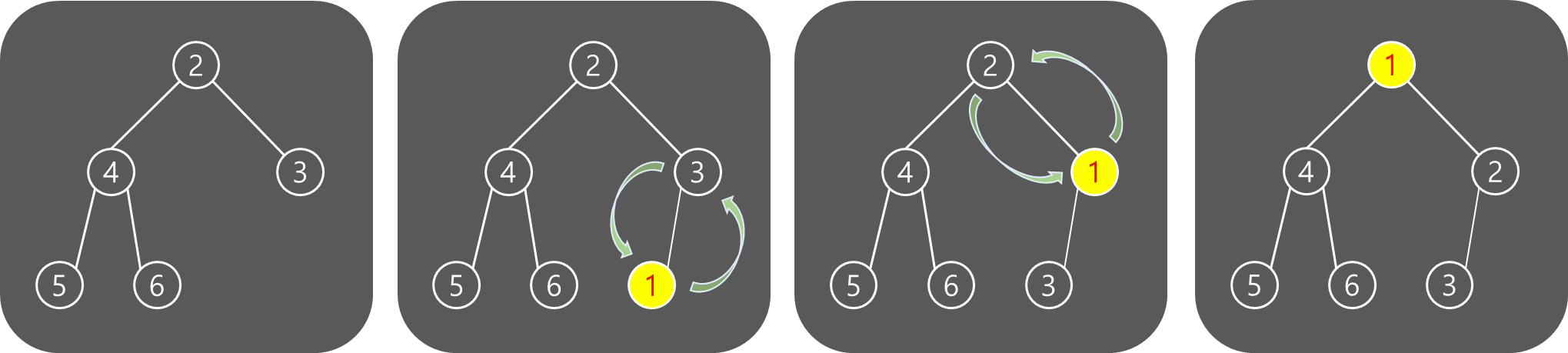
balance가 맞춰진 완전이진트리에서 이루어지기 때문에 한 레벨씩 루트(root)까지 올라간다면, 한 번 돌 때마다 절반씩 줄어 O(logn)의 시간복잡도를 가진다.
최소 힙의 노드 꺼내오기
- 최소 힙에서 노드를 요청할 때는 가장 작은 값을 요청한다. (그러려고 이렇게 정렬해서 만든거다..)
1. 최소 힙에서 가장 작은 값인 루트(root)를 꺼내온다.
2. 비어있는 루트(root)의 값을 채우기 위해 완전이진트리의 맨 마지막 값을 가져와 루트(root)에 채워준다.
3. 자신의 자식노드와 비교해서 정렬을 맞춘다. (두 개의 자식과 둘다 비교해서 더 작은 자식과 교환한다.)

이 작업도 마찬가지로 최대 O(logn)의 시간복잡도를 가진다
'Algorithm > Tree & Graph' 카테고리의 다른 글
| [알고리즘] 세그먼트 트리(Segment Tree) 알고리즘 동작 원리 및 구현하기 (0) | 2022.10.26 |
|---|---|
| [알고리즘] 다익스트라 알고리즘 (Dijkstra Algorithm) 동작 원리 및 구현하기 (1) | 2022.07.07 |
| [자료구조] Tree의 종류 및 Binary Tree의 3가지 순회 방법 간단하게 알아보기 (0) | 2022.06.03 |
| [자료구조] 그래프(Graph)의 개념 및 탐색 간단하게 알아보기 (1) | 2022.05.23 |


댓글